the pinhole model.
- Similar to thin lens model in Physics: central rays are not deviated.
- Assumes lens camera in focus.
- Useful approximation but ignores important lens distortions.
pinhole camera transformation
- add virtual image plane, where focal length is dist between camera center and image plane
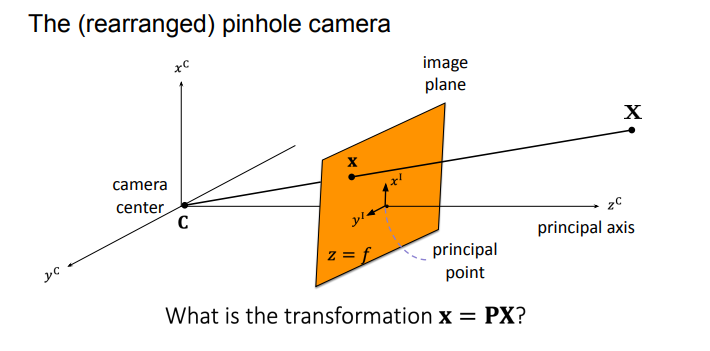
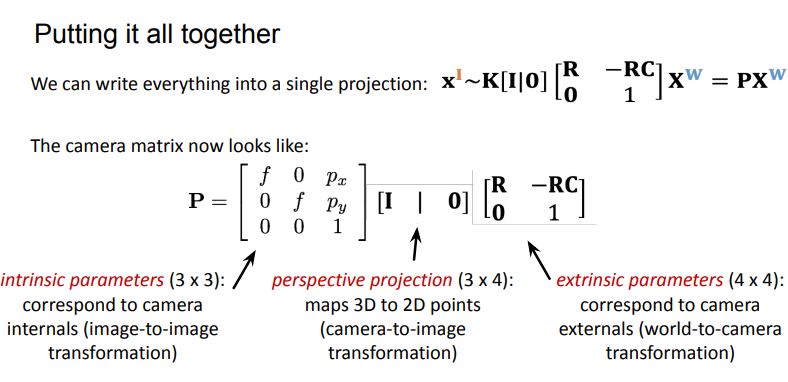
how do we project 3D points into 2D image coordinates? P is the answer.
-
P holds the camera intrinsics and extrinsics info
-
camera coordinates = world coordinates
-
want a camera matrix P such that the points get transformed to image coordinates
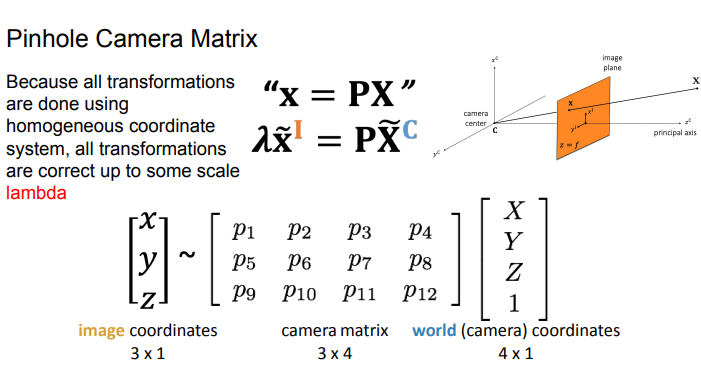
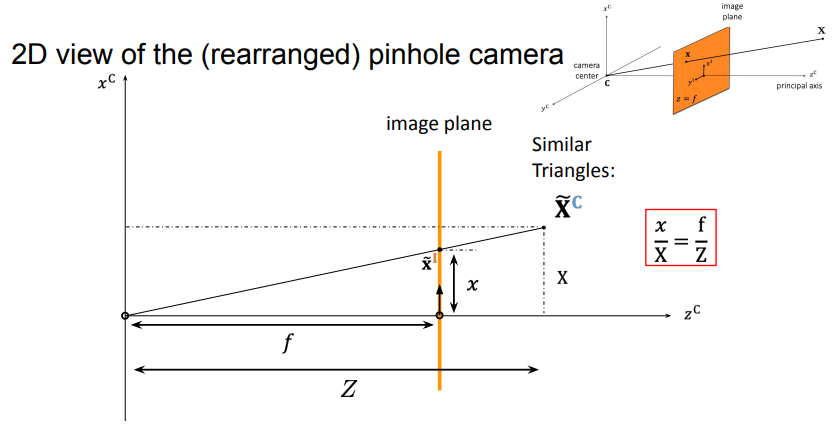

-
need to generalize matrix by translating from camera coordinate system to image coordinate system (diff image origins)
- camera coordinate system observes something on the image plane, at (x,y,z) cm
- the real image coordinate is in pixels (i,j) on a 2d plane
- this involves scaling + translation
-
the camera system is not at the origin of the world, so there is
- 3D point in world coordinates
- 3D point in camera coordinates
- 2D point in image coordinates
-
we need to align world coordinate system with camera coordinate system to do the math
- transformation
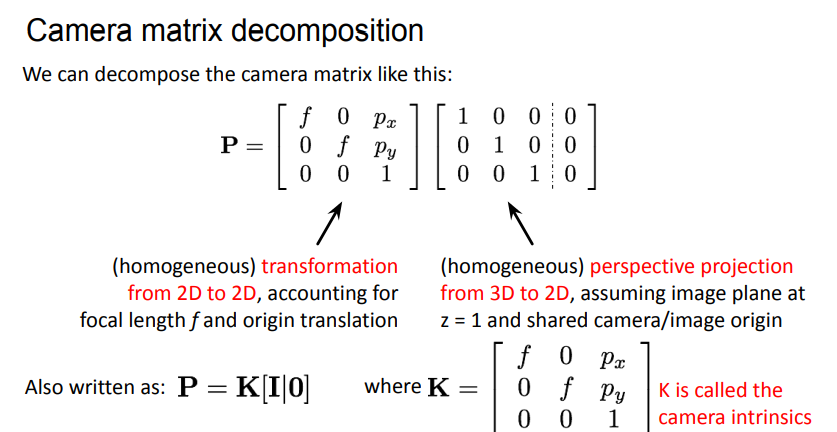
camera and lenses
- focal length
- aperture = light intensity of image pixels
- smaller aperture → less light passes thru → less diffraction and clearer image
also
- radial distortion = projective transformation
How do we estimate P and its components? camera calibration & pose estimation