Linear Discriminant Analysis (LDA)

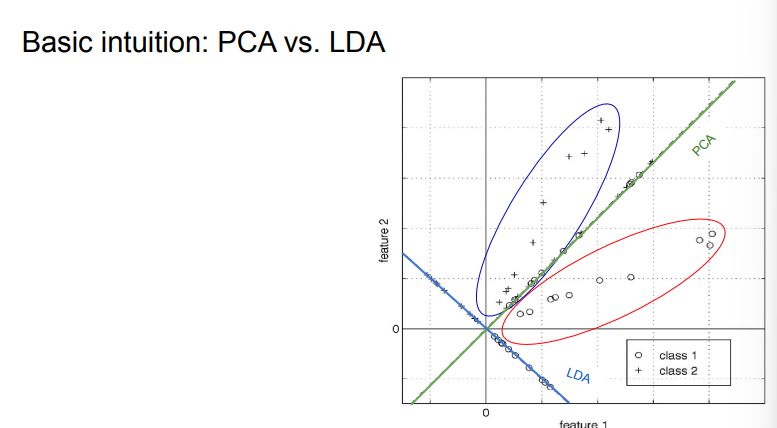
Linear transformation method that maximizes class separation - good for classification because it maximizes both variance and class discrimination - good for feature reduction in ML

LDA is a linear transformation method like principal component analysis (pca), but with a different goal.  

The main difference is that LDA takes information from the labels of the examples to maximize the separation of the different classes in the transformed space.

Therefore, LDA is not totally unsupervised since it requires labels. PCA is fully unsupervised.

• cares about maximizing both variance and class discrimination

In summary:

• PCA perserves maximum variance in the projected space.
• LDA preserves discrimination between classes in the project space. We want to
  • maximize scatter between classes (keep pts of same class close together)
  • minimize scatter intra class (push diff classes as far apart as possible) So, LDA is good for classification tasks, where we want reduced dimensions to still keep different categories distinct.

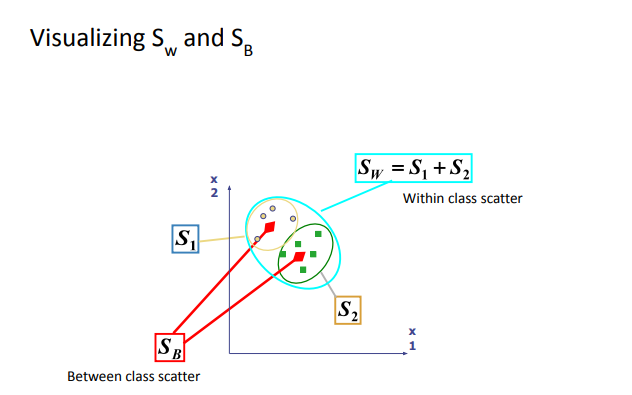
LDA optimizes the ratio $J(W)=\frac{\text{Between-class scatter}}{\text{Within-class scatter}}$

• between-class ($S_b$) measures how far apart class means are
• within-class ($S_w$) measures how tightly clustered each class is

ex. for two classes

$J(W)=\frac{({\mu }_1-{\mu }_2{)}^2}{{\sigma }_1^2+{\sigma }_2^2}$ this ratio should be as large as possible, meaning classes are far apart (large num) and individually compact (small denom)

the optimal projection W is given by eigenvectors+values of $S_w^{-1}{S}_b$

for C classes

• $S_w$ becomes sum of each class’s covariance matrix
• $S_b$ becomes sum of squared diffs between all class means Solution: take top e-vecs to project data to a lower-dim space

---