jennypng

Recent Notes

See 311 more →

principal component analysis (pca)

2 min read

  • The main goal of a PCA analysis is to identify patterns in data
  • PCA aims to detect the correlation between variables.
    • If a strong correlation between variables exists, attempt to reduce the dimensionality
    • Finding the directions of maximum variance in high-dimensional data and project it onto a smaller dimensional subspace while retaining most of the information. (see covariance)
  • geometric interpretation:
    • find projection that maximizes variance

intuition:

  • high dim data lives in some lower dim space?
  • covariance between two dims of fts is high - can we reduce to 1?

overview

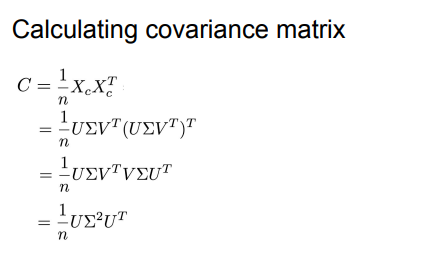
  • U is orthonormal, sigma^2 is diagonal → this is the eigenvalue decomp of C → we can calc eigenvectors of C using eigenvectors of X_c
    • eigenvecs of C are columns of U
    • eigenvals of C are diagonal entries of sigma
  • Sort eigenvalues in descending order and choose the k eigenvectors that correspond to the k largest eigenvalues where k is the number of dimensions of the new feature subspace (k≤d).
  • Construct the projection matrix W from the selected k eigenvectors.
  • Transform the original dataset X via W to obtain a k-dimensional feature subspace Y.

summary of pca by svd

  1. center data matrix
  2. compute its SVD
  3. PCs of covariance matrix C are columns of U

pca during training

  • an image is a point in high-dim space
  • if A is symmetric, it can be decomposed

limitations

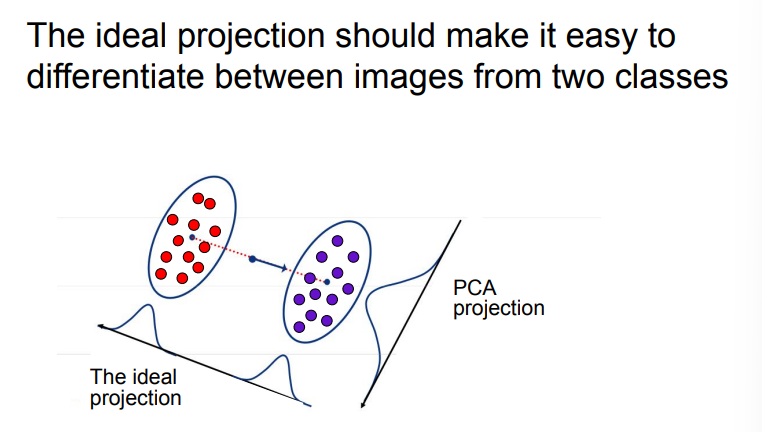
  • PCA works by projecting data onto the direction of maximum variance, preserving as much information as possible when compressing high-dimensional data.
    • maximizes ability to reconstruct each image, but not optimized for classification
  • but if we want to keep diff classes separable…

Graph View

Backlinks