-
Transform Edge Detections into lines
-
Detects lines/shapes
- only for shapes that can be expressed as an equation
-
Gives good detections even with noise or if shape is partially hidden
-
Input
- Output of some Edge Detection
- pixels that partially describe boundary of objects
- Output of some Edge Detection
-
We want to find sets of pixels that make up straight lines
-
assume n=y, m=x
f[n,m] = f[y,x]
-
We don’t know which pairs of edge points belong to the same line.
- Do two points lie on the same line?
-
BUT this fixes that
-
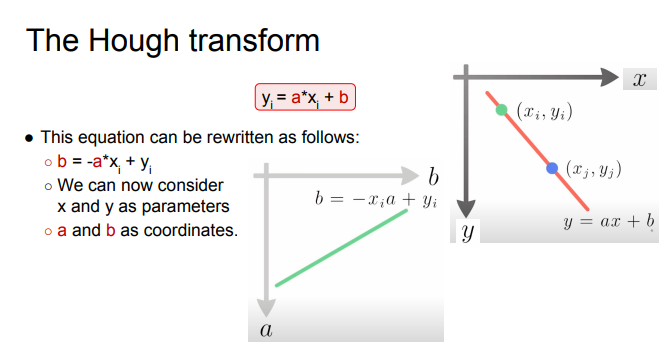
all straight lines passing through a point have
-
rewrite as
-
we consider x and y as parameters, a and b as coordinates
-
so one point will give us a line in (a,b) space
-
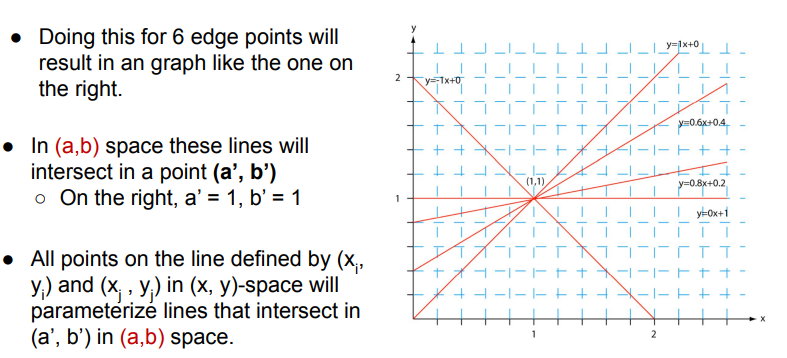
Ex. if 6 edge points intersect at (1,1)
- there might be a line with y-intercept 1, slope 1
- but not all intersections are valid lines
- two edge points not in a real edge could still intersect
- How do we identify intersections that are belong to the same edge versus random points?
-
More lines intersecting at (a’,b’), the more likely y=a’x+b’ is a real edge
- Converts from one domain to another, counts in second domain
- voting algorithm , vote for buckets of intersection in (a,b) space
- each point votes for compatible models

- each point votes for compatible models
- voting algorithm , vote for buckets of intersection in (a,b) space
- Converts from one domain to another, counts in second domain
-
Can also represent lines as polar coordinates
- Can transform from (x,y) to curves in (p, theta) space
- reason to do this: you can’t represent horizontal/vertical lines in (a,b) due to no y-intercept?
- in curve space,
remarks
- advantages
- simple
- ez
- can handle missing/occluded data
- adaptable to other shapes than lines
- disadvantages
- complex for high parameter shapes
- looks for one shape
- can be fooled by “apparent lines”
- length/pos of line segment can’t be determined
- co-linear line segments cannot be separated
- runs in O(N^2) coz considers all point pairs, iterates through features and parameters
- noisy points vote too, but typically their votes are inconsistent with majority of good edge points (outliers)