definition
combine 2 discrete-time signals to produce a third
the 2D convolution of an image and a kernel is defined as follows:
Or equivalently,
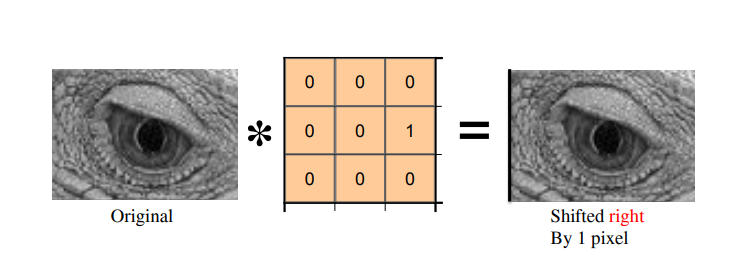
- convolution intuition examples
- associative (allows cascading filters) and commutative
- linear

- ^ defines 2D convolution of input image
f[n,m]with kernelh[n,m]- n-k and m-l slide the flipped kernel across the image (non-flipped is cross correlation)
- flipping is just part of the definition of convolution…
2D discrete convolution
- convolutions are defined so that you have to flip the kernel
- 2D convolution

- k and l are indices from input image, n and m are indices of output
f[k,l]is the input image- given kernel (filter (kernel))
h[k,l], we need to fold it about the origin (flip) and shift it to align with the current pixel: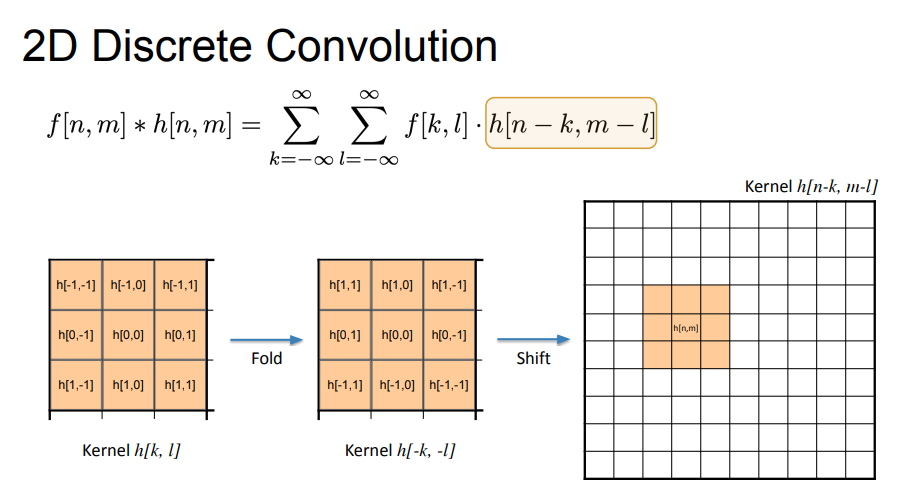
- multiply each value aligned with image,
- we need to flip the kernel horizontally and vertically
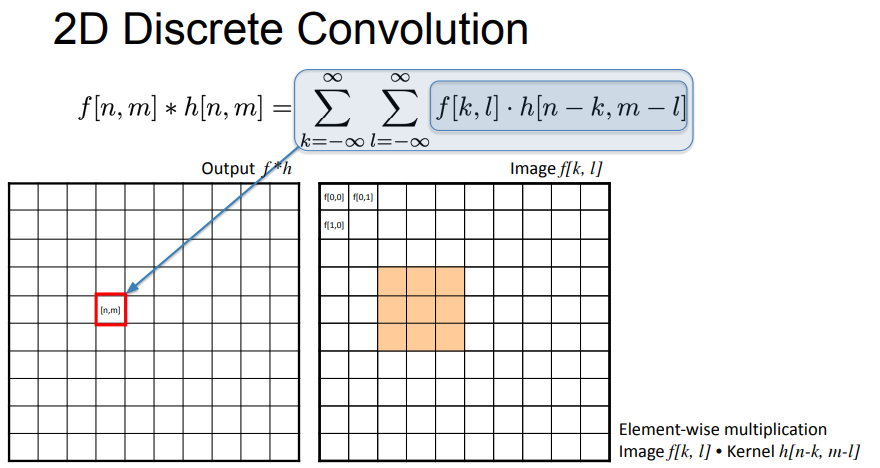
- to get n-k and m-l???
- to get n-k and m-l???
- ^ shifts right because the kernel is flipped, and the leftmost column is negated
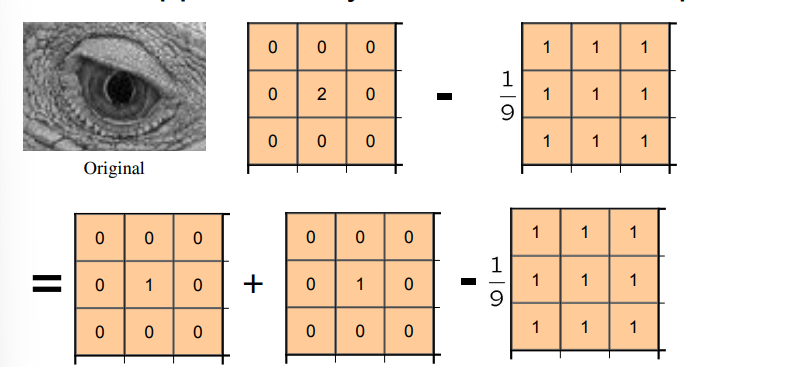
- ^ stacking filters -
implementation
- remember to flip kernel
- (m,n) indexes into output image, (i,j) indexes into kernel
- the original image is indexed so the desired pixel is lined up with the center of the kernel
naive
Hi, Wi = image.shape Hk, Wk = kernel.shape out = np.zeros((Hi, Wi))
// flip kernel // alt: np.flip(kernel, axis=(0,1)) kernel = kernel[::-1, ::-1]
// convolve - m,n is output indices, i,j is kernel incices // row,col is the index of the image to look at (offset by centering the kernel)
for m in range(Hi): for n in range(Wi): for i in range(Hk): for j in range(Wk): row = m + (i - Hk // 2 ) col = n + (j - Wk // 2) if 0 ⇐ row < Hi and 0 ⇐ col < Wi: out[m][n] += kernel[i][j] * image[row][col]
return out
better
- zero-pad image based on kernel size
- use np.sum on kernel * pixel neighbors
other
1D convolution:
