reconstruct 3D structures from collection of 2D images taken from diff viewpoints
triangulation: 2D points to 3D structure
Given:
- Two or more images of the same scene.
- Known camera matrices P and P’ (camera intrinsics and extrinsics)
- Corresponding 2D points x and x’ in images
Goal: Find the 3D point X that projects to x and x’
and
-
applying camera matrix to 3D point gives pixel point
-
homogeneity , lose depth
-
backprojection
- apply pseudo-inverse of P on x, and connect the points — this doesn’t give full 3D position tho since we don’t know depth
-
fix: we enforce co-linear constraints:
- cross-product
- this equality removes scale factor from
-
with two linear equations per view and at least two views, we can solve for X with singular value decomposition (SVD) (similar to camera calibration & pose estimation)
-
triangulation requires two cameras to have enough equations to solve for all unknowns
- rays intersect at 3D object point
challenges
- noise may prevent rays from intersecting well
- fix: add more rows to matrix with more cameras
- singular value decomposition (SVD) provides least-squares solution (best fit)
epipolar geometry: constraints between views
by enforcing constraints, reduce complexity of matching points between images
- baseline: line connecting camera optical centers O and O’
- epipoles (e,e’): where baseline intersects the image planes
- projection of o’ on the image plane
- epipolar plane: plane formed by baseline and 3D point X
- epipolar line: intersection of epipolar plane and image plane (all possible matches are here) epipolar constraint
- for point x in first image, its match x’ in second image must lie on epipolar line l’
- reduces search space to 1D, so matching is more efficient importance
- no need for depth sensors - pure geometry-based 3D reconstruction
- fundamental
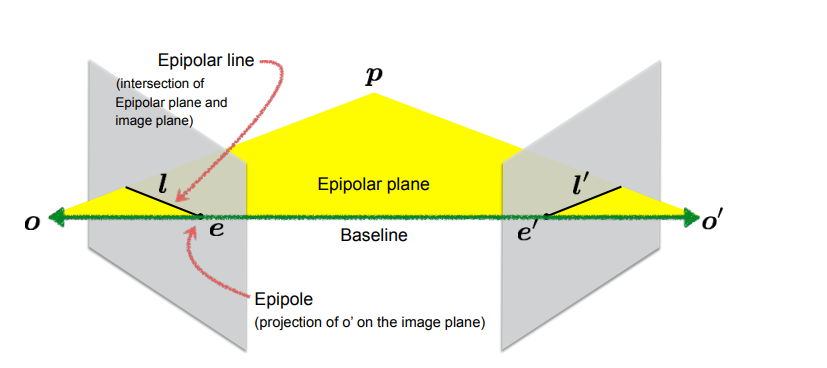
Where are epipoles?
essential (E) & fundamental (F) matrices
encodes camera motion
- - encodes rotation and translation between cameras
- constraint: for points in 2D camera coordinates,
- properties
- rank = 2 (due to cross-product)
- singular values
- multiplying a point by E tells us the epipolar line in the second view
- diff from image homographies coz
- E maps point to line
- homography maps point to point
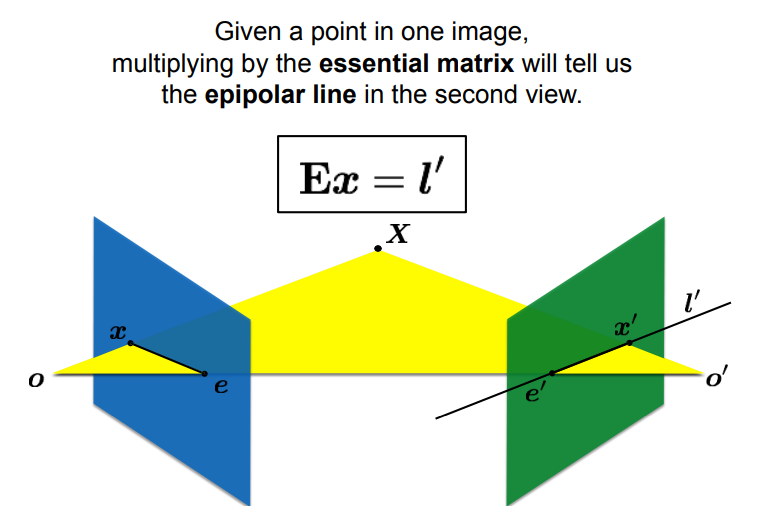
-
- constraints: for points in image coordinates,
- estimation:
- use 8-point algorithm and RANSAC
- solvable from correspondences, doesn’t need known camera poses
- Recovering camera motion
- decompose E into R and t (up to scale ambiguity)
- triangulate 3D points with recovered poses
SfM Pipeline
combines everything for full 3D reconstruction
Given many images, how can we
- figure out where they were all taken from?
- build a 3D model of the scene?
Calibrate → Triangulate
- Feature Matching
- extract features
- find correspondences
- Estimate motion between images by calculating F
- use RANSAC for outliers
- Recover poses
- decompose F (or E) into R and t
- Triangulate 3D points to estimate 3D structure
- solve for X with svd
- bundle adjustment
- non-linear optimization
- for added views
- determine motion using all known 3D points that have correspondence in new image
- add structure by estimating new points in new image