Structure from Motion

reconstruct 3D structures from collection of 2D images taken from diff viewpoints

triangulation: 2D points to 3D structure

Given:

• Two or more images of the same scene.
• Known camera matrices P and P’ (camera intrinsics and extrinsics)
• Corresponding 2D points x and x’ in images

Goal: Find the 3D point X that projects to x and x’

$x=PX$ and $x^{\prime }=P^{\prime }X$

• applying camera matrix to 3D point gives pixel point

• homogeneity , lose depth

• backprojection

  • apply pseudo-inverse of P on x, and connect the points — this doesn’t give full 3D position tho since we don’t know depth

• fix: we enforce co-linear constraints:

  • $x\times (PX)=0$ cross-product
  • this equality removes scale factor from $x=\alpha PX$

• with two linear equations per view and at least two views, we can solve for X with singular value decomposition (SVD) (similar to camera calibration & pose estimation)

• triangulation requires two cameras to have enough equations to solve for all unknowns

  • rays intersect at 3D object point

challenges

• noise may prevent rays from intersecting well
  • fix: add more rows to matrix with more cameras
• singular value decomposition (SVD) provides least-squares solution (best fit)

epipolar geometry: constraints between views

by enforcing constraints, reduce complexity of matching points between images

• baseline: line connecting camera optical centers O and O’
• epipoles (e,e’): where baseline intersects the image planes
  • projection of o’ on the image plane
• epipolar plane: plane formed by baseline and 3D point X
• epipolar line: intersection of epipolar plane and image plane (all possible matches are here) epipolar constraint
• for point x in first image, its match x’ in second image must lie on epipolar line l’
• reduces search space to 1D, so matching is more efficient importance
• no need for depth sensors - pure geometry-based 3D reconstruction
• fundamental

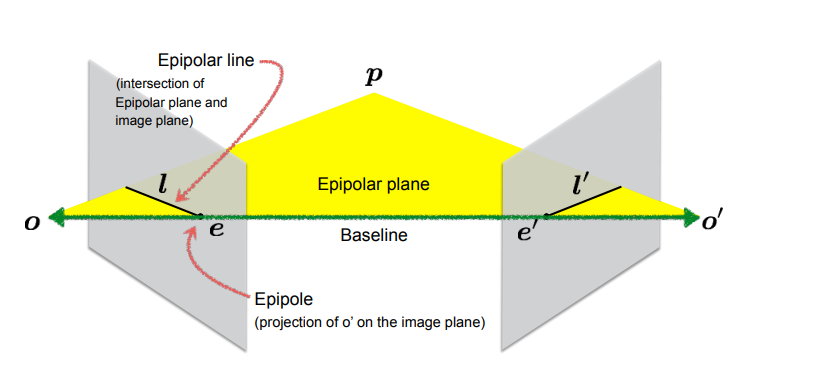
Where are epipoles?

essential (E) & fundamental (F) matrices

encodes camera motion

• $E=[t]\times R$ - encodes rotation and translation between cameras
  • constraint: for points in 2D camera coordinates, $x^{\prime T}Ex$
  • properties
    • rank = 2 (due to cross-product)
    • singular values
  • multiplying a point by E tells us the epipolar line in the second view
  • diff from image homographies coz
    • E maps point to line
    • homography maps point to point
• $F=K^{\prime -T}E{K}^{-1}$
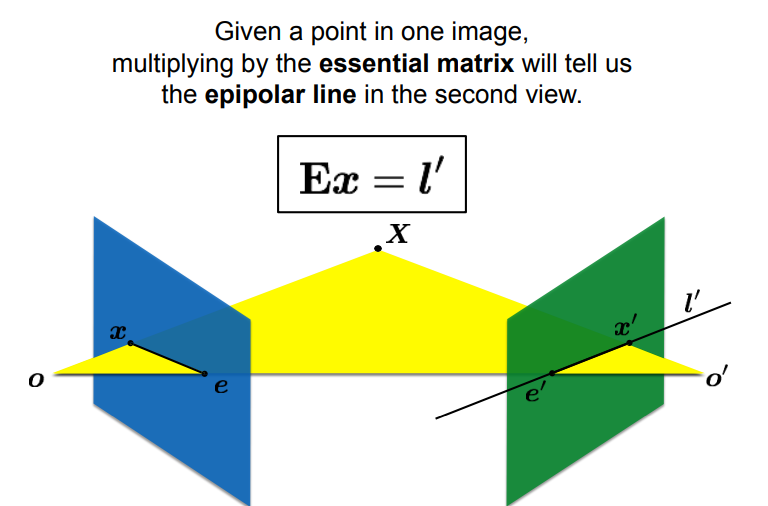
  • constraints: for points in image coordinates, $x^{\prime T}Fx=0$
  • estimation:
    • use 8-point algorithm and RANSAC
    • solvable from correspondences, doesn’t need known camera poses
• Recovering camera motion
  • decompose E into R and t (up to scale ambiguity)
  • triangulate 3D points with recovered poses

SfM Pipeline

combines everything for full 3D reconstruction

Given many images, how can we

• figure out where they were all taken from?
• build a 3D model of the scene?

Calibrate → Triangulate

1. Feature Matching
   1. extract features
   2. find correspondences
2. Estimate motion between images by calculating F
   1. use RANSAC for outliers
3. Recover poses
   1. decompose F (or E) into R and t
4. Triangulate 3D points to estimate 3D structure
   1. solve for X with svd
5. bundle adjustment
   1. non-linear optimization

• for added views
  • determine motion using all known 3D points that have correspondence in new image
  • add structure by estimating new points in new image