singular value decomposition (SVD)

• SVD image compression works by decomposing the image matrix into three matrices (U, Σ, and V). 

$U\Sigma V^T=A$

• U and V are rotation matrices
• $\Sigma$ is a scaling matrix

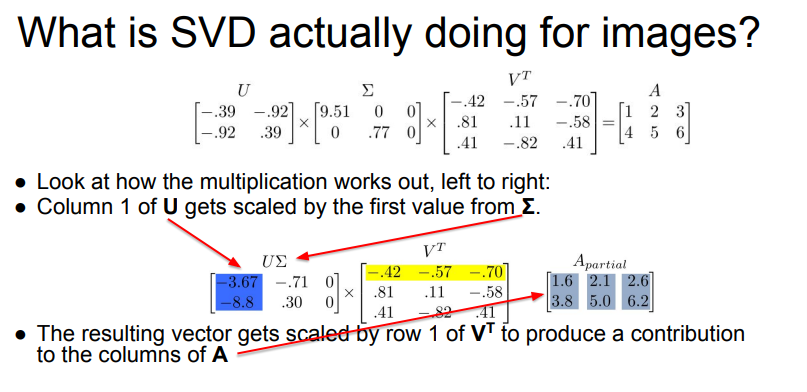
• each product of (col i of U) * (val i from sigma) * (row i of V^T) produces a component of final A

• A is a linear combo of cols of U

  • using all columns of U, we can rebuild og matrix perfectly
  • but real-world, we get first few columns of U = principal components
    • show major patterns
  • rows of V show how principal components are mixed to produce cols in the matrix

• It approximates the original image with a lower-rank matrix → image compression by taking first k principal components

  • reduces the amount of data needed to represent the image while retaining its key features.

• use to solve $AX=0$

principal component analysis (pca)

1. columns of U are principal components (orthogonal directions of variance)
2. sigma contains singular values (importance of each component)