Keypoint localization - repeatable, precise, and interesting (distinct) - corner detection!!!
-
Look for 2D signal changes
- things change a lot at corners
- changes can be detected with similar concepts from Edge Detection and linear shift invariant (LSI)
-
The Image gradient around a corner has 2+ dominant directions
- repeatable and distinctive
- significant change in all directions
-
Corners are distinctive key-points
- x and y derivatives are large
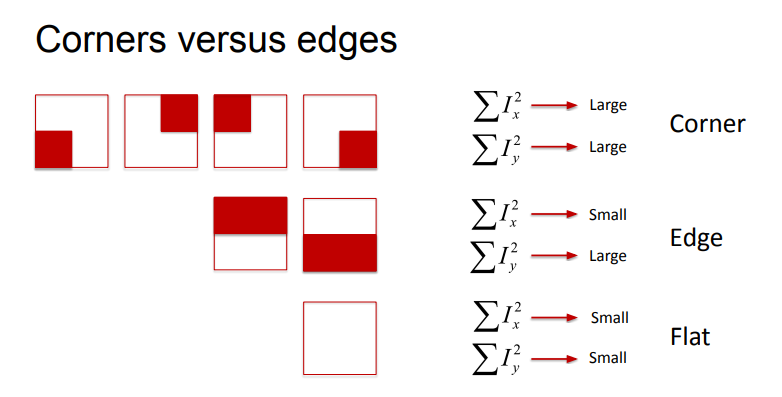
- x and y derivatives are large
-
but how do we generalize corners to any direction?
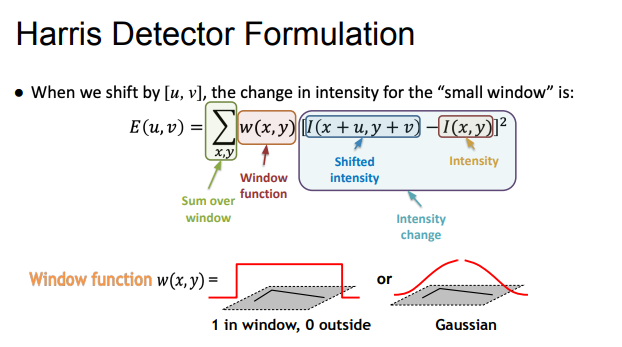
formulation
- Find windows/patches that result in large change of pixel values when shifted in any direction

- E can be rewritten as
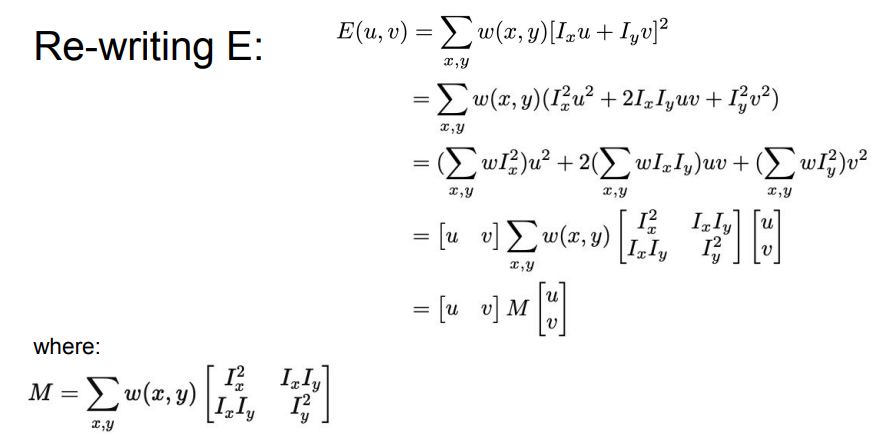
- M is at every pixel, window function (to only look within window) multiplied with matrix comprised of gradient wrt x and wrt y
- expression E for change in intensity function - also equation for an ellipse?
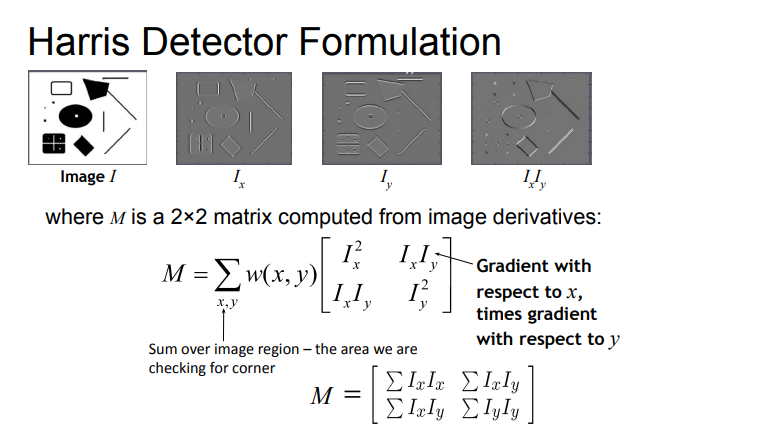
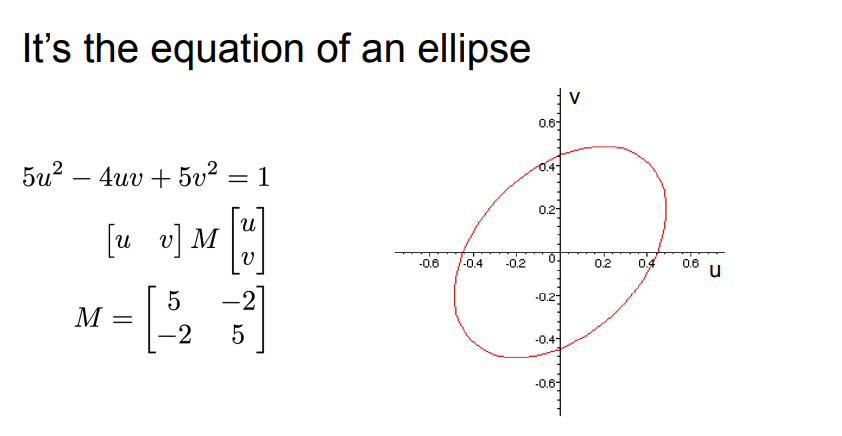
- when the diagonals of M are large, it becomes more like a circle..? ( every direction is large )

- a rotated corner is an axis-aligned corner rotated
- if we just look at the scale of the eigenvalues, we can tell if something is a corner regardless of its rotation
- lambda1 and lambda2 will be large

- Calculating eigenvalues is expensive → corner response function
- window function
summary
- compute x and y derivatives of image
- compute products of derivatives at each pixel
- compute matrix M at each pixel
- compute corner response at each pixel
- output corner response map

Properties
-
Results are good for finding correspondence matches between images
-
has
- translation invariance
- rotation invariance
- corner response function is invariant
- not invariant to scale
- in a bigger image, the points would be classified as edges